近日,公司青年教师盛洲博士在《Mathematics of Computation》上发表Stiefel流形上齐次多项式优化的最新研究成果。《Mathematics of Computation》由美国数学学会创办,是计算数学领域国际顶级期刊,中国数学会期刊分级目录(2020年)T1期刊。公司为论文第一单位,盛洲博士、深圳市大数据研究院李建泽博士和南京航空航天大学倪勤教授合作完成,盛洲博士为论文第一作者,李建泽博士为通讯作者。研究工作得到了国家自然科学基金、安徽省自然科学基金、广东省自然科学基金等项目资助。
Stiefel流形上齐次多项式优化在科学工程计算以及数据科学等领域有着广泛的应用, 例如独立成分分析、稀疏主成分分析、正交Procrustes问题和Kohn-Sham 总能量极小化问题等。其中,Kohn-Sham总能量极小化是材料科学中的一个重要问题,即在Stiefel流形上极小化离散的Kohn-Sham 总能量泛函。Jacobi类算法是求解Stiefel流形上齐次多项式优化问题的一类重要算法,已经被用来求解张量的联合近似对角化等问题。然而,该算法的全局收敛性未被充分研究。
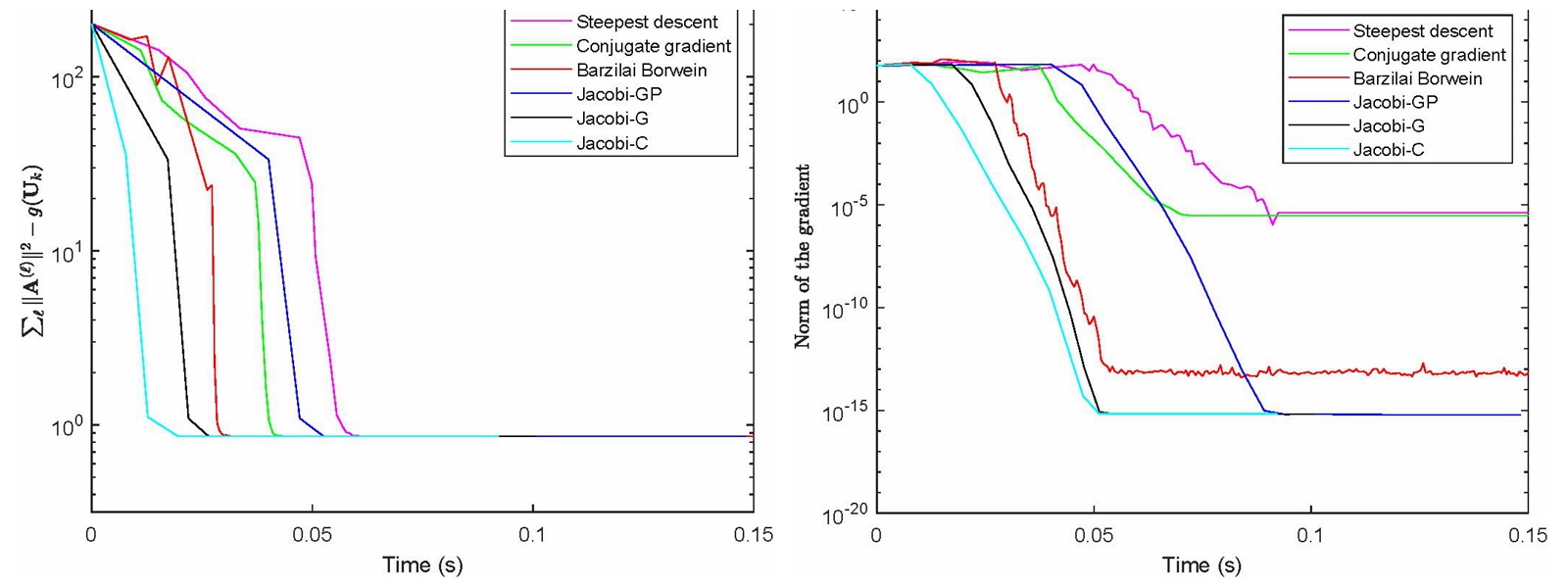
(8个10*10对称矩阵同时对角化问题不同算法关于cpu时间的数值比较)
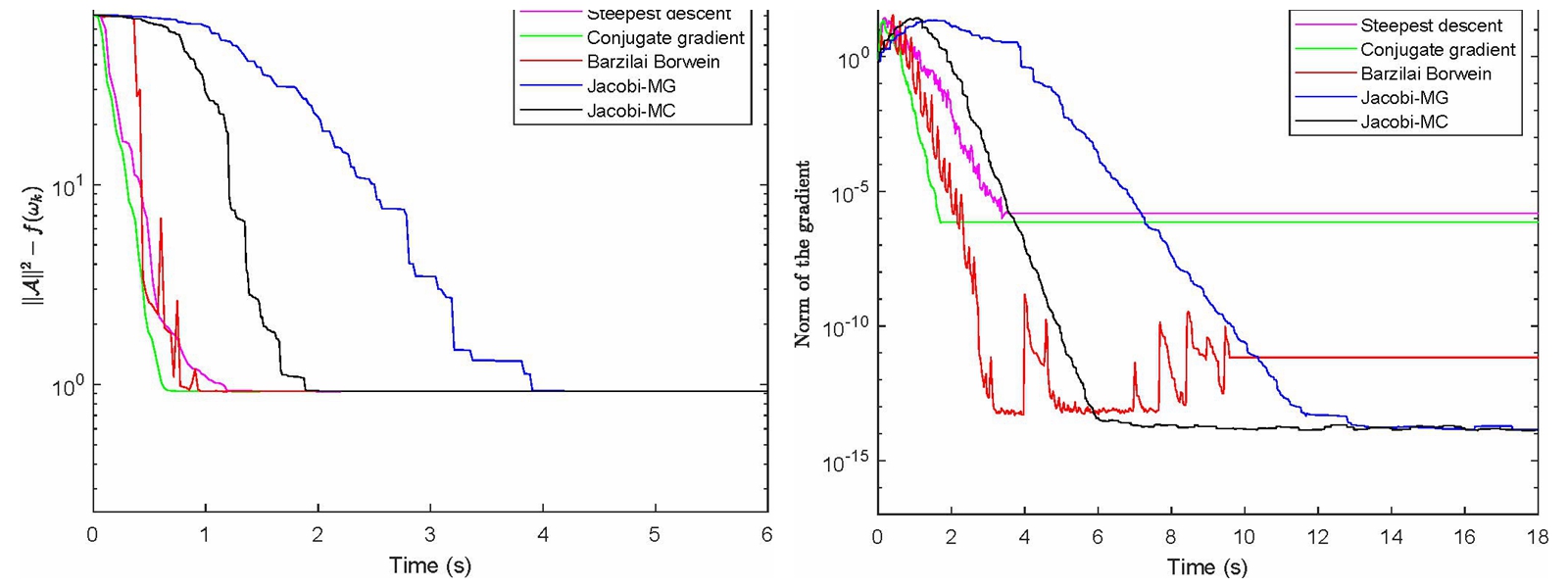
(5*5*6*6非对称张量对角化问题不同算法关于cpu时间的数值比较)
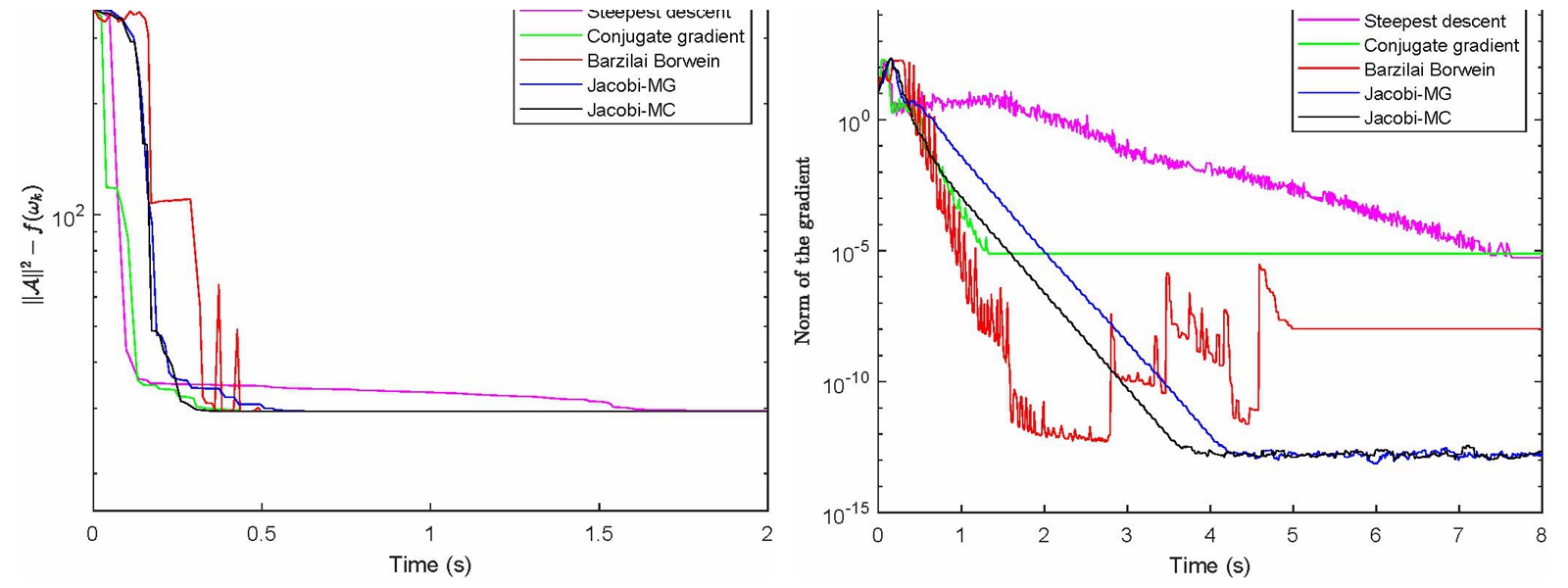
(3*3*3*3非对称张量对角化问题不同算法关于cpu时间的数值比较)
本研究给出了Jacobi类算法对于求解Stiefel流形上齐次多项式优化问题全局收敛性的证明。在Jacobi类算法的子问题可以写为单个二次型的情形下,提出了2个新的收敛性条件,并将1个已有条件进行推广,从而在其中任意1个条件满足时,证明了算法的全局收敛性。特别地,对于非对称张量的联合近似对角化问题,这两个新的条件是满足的,为Jacobi类算法在Stiefel流形上齐次多项式优化问题中的应用提供了理论保证。
论文链接:https://doi.org/10.1090/mcom/3834
(撰稿:刘小弟 审核:杨二光)


